EM Algorithm for Mixture Model

Ian Arriaga-MacKenzie

Last updated on Jun 3, 2022

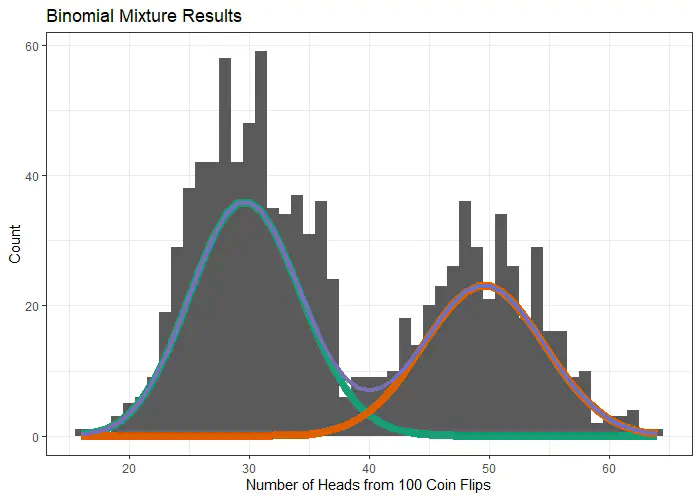
We can generate a population for a binomial mixture under the following assumptions: That we have a number n of true cases out of a possible number N total, and that these have a binomial distribution with $π_{i}$ probability of being from each distribution.

This is easier to visualize with a ‘coins in a pot’ example. Say we have a pot filled with two types of coins, each type of coin having its own probability of heads. We pull a number of coins S from the pot, flip each coin N times and record the number of n heads. Under these assumptions, the probability of seeing n heads for each coin would be:

P (n | N, Θ) = π_{1} Binom (n | N, θ_{1}) + π_{2} Binom (n | N, θ_{2})

or more generally for K different types of coins

P (n | N, Θ) = \sum_{k = 1}^{K} π_{k} Binom (n | N, θ_{k})

where $θ_{k}$ is the probability of heads for each type of coin. Therefor the log-likelihood for our parameters is:

L (Θ | X, Z) = l n P (X, Z | Θ)

Where $Θ_{k}$ represents the set of $π_{k}, θ_{k}$ , X represents the set of heads and total coin flips, and Z represents the set of coin proportions and heads proportions. So the Auxiliary Function is:

Q (Θ, Θ_{o}) = E [l n L (Θ | X, Z) | X, Θ_{o}]

and our expectation is:

E [l n P (X, Z, | Θ) | X, Θ_{o}] = \sum_{z_{i} = 1}^{K} l n P (n_{i}, z_{i} | Θ) \cdot P (z_{i} | n_{i}, Θ_{o})

where

P (z_{i} = k | n_{i}, Θ_{o}) = \frac{P (z_{i} = k, n_{i} | Θ_{o})}{P (z_{i}, n_{i} | Θ_{o})} = \frac{π_{k, o} Binom (n_{i} | N_{i}, θ_{k, o})}{\sum_{l = 1}^{K} π_{l, o} Binom (n_{i} | N_{i}, θ_{l, o})}

We can then use the following expressions to update $π$ and $θ$ until convergence.

π_{m} = \frac{1}{S} \sum_{i = 1}^{S} P (z_{i} = m | n_{i}, Θ_{o})

θ_{m, S} = \frac{\sum_{i = 1}^{S} n_{i} \cdot P (z_{i} = m | n_{i}, Θ_{o})}{\sum_{j = 1}^{S} N_{j} \cdot P (z_{j} = m | n_{j}, Θ_{o})}

EM Algorithm for Mixture Model

Ian Arriaga-MacKenzie

Statistics and Computational Mathematics